2018安徽教师招聘中学数学真题及答案解析
一、单项选择题。下列各题备选答案中只有一项符合题意，请将其选出。（共10小题，每小题4分，共40分）
1.i是虚数单位，
=（
）。
A、-8
B、8
C、-8i
D、8i
2.已知向量
=（2，1），
=（3，4），
=（1，m），若实数λ满足+=λc，则λ+m=（ ）。
A、5
B、6
C、7
D、8
3.在△ABC中，D是BC上一点，CD=3BD，AB=AC=4，AD=
，则BD=（
）。
A、
B、
C、2
D、6
4.已知圆C：
，过点P（2，3）作直线l交圆C于A，B两点，当弦AB的长度最小时，直线的方程为（ ）。
A、x+y-5=0
B、x+2y-8=0
C、x-y+1=0
D、x-2y+4=0
5.若函数f（x）=Asin（x+φ）（A>0）的部分图象如图所示，则f（x）的单调递增区间为（ ）。
A、<2kπ-1，2kπ>，k∈Z
B、<2k-1，2k>，k∈Z
C、<2kπ-π，2kπ>，k∈Z
D、<2k-π，2k>，k∈Z
6.已知定义在R上的偶函数f（x）在[0，+∞）上单调递增，f（1）=0，则f（x-2）≥0的解集是（ ）。
A、<1，3>
B、<1，2）u（2，3>
C、<1，2>U<3，+∞）
D、（-∞，1>U<3，+∞）
7.从集合{2，3，4，8，9}中先后取出两个不同的数构成有序数对（a，b），使得
是有理数的概率为（
）。
A、0.6
B、0.4
C、0.3
D、0.2
8.《义务教育数学课程标准（2011年版》》中描述结果目标的行为动词主要包括了解、理解、掌握和（ ）。
A、运用
B、体验
C、经历
D、探索
9.《义务教育数学课程标准（2011年版）》中指出，信息技术的发展对数学教育的价值、目标、内容以及教学方式产生了很大的影响，下列说法正确的是（ ）。
A、现代信息技术可以完全替代原有的教学手段
B、在应用现代信息技术时，教师不需要课堂教学板书设计
C、现代信息技术的真正价值在于实现原有的教学手段难以达到甚至达不到的效果
D、现代信息技术的应用不利于培养学生的几何直观
10.《义务教育数学课程标准（2011年版）》中指出，对于学生基础知识和基本技能达成情况的评价必须准确把握课程内容中的要求，下列做法不符合要求的是（ ）。
A、在设计试题时，应淡化特殊的解题技巧，不出偏题怪题
B、在考试时，几何命题的证明应以“图形的性质”中所列的基本事实和定理作为依据
C、考查的内容一般应限定在必学范围内
D、选学内容“三元一次方程组”可以列入考试范围
二、填空题。根据题干内容，在横线中填写正确答案。（共5小题，每小题4分，共20分）
11.若正数a，b满足a+b+ab=3，则a+b的最小值为________。
12.计算：
=________。
13.设D是由曲线y=
，直线y=x及y=2围成的有界区域，则D的面积为________。
14.计算：行列式
=________。
15.《义务教育数学课程标准（2011年版）》中把课程总目标分为知识技能、数学思考、问题解决、情感态度四个方面，下列表现属于情感态度方面的是。（写出所有正确结论的编号）
①积极参与数学活动，对数学有好奇心和求知欲；
②能独立思考，体会数学的基本思想和思维方式；
③有克服困难的勇气，具备学好数学的信心；
④在与他人合作和交流过程中，能较好地理解他人的思考方法和结论；
⑤敢于发表自己的想法，勇于质疑，勇于创新。
三、解答题。根据题目要求，回答问题。（共5小题，每小题8分，共40分）
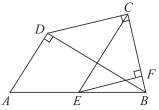
16.一副三角板按如图方式摆放，得到四边形ABCD，其中∠ADB=∠BCD=90°，∠A=60°，∠CBD=45°，E为AB的中点，过点E作EF⊥CB于点F。
（1）求证：AD∥EC；
（2）当AD=4时，求线段EF的长。
（2）当AD=4时，求线段EF的长。
17.已知数列{
}满足
=1，
-（n+1），=
。
（1）求数列|an|的通项公式；
（2）求证：
。
18.如图1，已知圆O的直径AB=2，上半圆弧上有一点C，∠COB=60°，点P是劣弧AC上的动点，点D是下半圆弧的中点，如图2，现以AB为折线，将上、下半圆所在的平面折成直二面角，连接PO，PC，PD，CD。
（1）当AB∥平面PCD时，求线段PC的长；
（2）当三棱锥P-COD的体积最大时，求二面角C-PD-O的余弦值。
19.在平面直角坐标系xOb中，曲线C：
与直线y=kx+a（a≠0）交于A，B两点。
（1）若·
=0，求a的值；
（2）若·=-4，求AB中点的轨迹方程。
20.已知函数f（x）=ln（1-x）。
（1）求曲线y=f（x）在x=0处的切线方程；
（2）判断函数g（x）=f（x）+
的零点个数。
四、案例分析题。阅读材料，回答问题。（共1小题，每小题10分，共10分）
（一）
“三角形的稳定性”的教学片段：王老师在组织一堂主题为“利用三角形的稳定性解决实际问题”的活动课时，他给同学们提出这样一个问题：一个纱门，它四边的榫卯老化，导致纱门变形，如何让门框固定？王老师用木条钉做了几个纱门模型，如图（1），交给四个学习小组，并配给一点铁钉、木条、钉锤......请大家用所学的数学知识来解决这个问题。
活动结束后，四个小组汇报了解决问题的方案，其中有三组用了王老师的预设方案（如图（2）：沿纱门对角线端点钉上一根木条，纱门变成两个三角形，纱门能够固定，但有一个小组却拿出了王老师没料想到的方案（如图（3））：用一根短木条，将两端钉在纱门相邻的两边上，纱门也固定。
师：你们为什么选择这种方案来解决问题呢？
生1：节约用料，且钉上短木条，对纱门美观影响小。
师：那你能说一下其中的道理吗？
生1：短木条与纱门两边组成△CEF，三角形的稳定性能使门框固定。
生2：老师，门框固定，五边形 ARFED也同样具有稳定性吗？这与我们以前知道的五边形不稳定性相矛盾呀！
面对生2的发问，王老师和全班同学无法回答，陷入沉思......
回读以上材料，回答以下问题：
21.
（1）请你对生2的疑问做出合理的解释。
（2）针对本节课出现的情况，如果你是王老师，如何应对？
五、教学设计题。请根据所提供的教学材料和相关情况，按要求完成教学设计。（共1小题，每小题10分，共10分）
（二）
《普通高中数学课程标准（实验）》指出：数学探究是指学生围绕某个数学问题，自主探究、学习的过程，这个过程包括：观察分析数学事实，提出有意义的问题，猜测探索适当的数学结论或规律，给出解释或证明。
素材：在单位圆中，角α的终边与单位圆的交点记为P，角Π-a的终边与单位圆的交点记为
，利用P与坐标间的关系，可以得到角α与角Π-a之间的三角函数关系，即角Π-a的诱导公式。
22.
（1）写出角π-α的诱导公式（三个）；
（2）依据上述素材和要求，试撰写一份关于“角π-α的诱导公式”的教学过程设计。（只要求写出教学过程，突出数学探究）
注：篇幅有限，答案及解析请下载试卷后查看。