2018江西教师招聘初中数学真题及答案解析
一、单项选择题。下列各题备选答案中只有一项符合题意，请将其选出。（共50小题，每小题1分，共50分）
1.数学是研究（ ）和空间形式的科学。
A、代数运算
B、逻辑推理
C、数量关系
D、抽象思维
2.义务教育阶段的数学课程是培养公民素质的基础课程，具有基础性、（ ）和发展性。
A、阶段性
B、重要性
C、连续性
D、普及性
3.教学活动是师生积极参与、交往互动、（ ）的过程。
A、共同发展
B、教学相长
C、共同成长
D、共同进步
4.教师教学应该以学生的认知发展水平和（ ）为基础，面向全体学生，注重启发式和因材施教。
A、已有的知识
B、生活经验
C、已有的经验
D、心理特征
5.学习评价的主要目的是为了全面了解学生数学学习的过程和结果，（ ）和改进教师教学。
A、激发学生兴趣
B、激励学生学习
C、检测学习效果
D、激发学习动力
6.“综合与实践”是一类以问题为（ ），以学生自主参与为主的学习活动。
A、对象
B、导向
C、目标
D、载体
7.运算能力主要是指能够根据（ ）和运算律正确地进行运算的能力。
A、法则
B、公式
C、定理
D、公理
8.数学教学要整体实现课程目标，要把知识技能、数学思考、（ ）、情感态度四个方面目标有机结合
A、过程方法
B、提升素养
C、积累经验
D、问题解决
9.学生主体地位的真正落实，依赖于教师的（ ）有效发挥。
A、引领作用
B、有效教学
C、主导作用
D、平等交流
10.义务教育的第三学段评价结果的呈现可以采用（ ）评价和等级（或百分制）评价相结合的方式。
A、考试
B、描述性
C、建立档案
D、学分制
11.-2018的相反数是（ ）。
A、±2018
B、-2018
C、-2019
D、2018
12.中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，“一带一路”某次会议参加的人数约为180000人，这个数用科学计数法表示为（ ）。
A、
B、
C、
D、
13.已知点A（a，-1），与点B（5，b）关于坐标原点对称，则实数a，b的值是（ ）。
A、a=5，b=1
B、a=-5，b=1
C、a=5，b=-1
D、a=-5，b=-1
14.在一些汉字的美术字中，有的是轴对称图形，下面四个美术字可看作轴对称图形的是（ ）。
A、城
B、信
C、友
D、善
15.面积为5的正方形边长在（ ）。
A、0到1之间
B、1到2之间
C、2到3之间
D、3到4之间
16.小红要购买珠子串成一条手链，黑色珠子每个5元，白色珠子每个4元，要串成如图所示的手链，小红购买珠子要花费（ ）。
A、31元
B、32元
C、36元
D、40元
17.二元一次方程组
的解为（ ）。
A、
B、
C、
D、
18.在函数
中，自变量x的取值范围是（
）。
A、x>6
B、x≥6
C、x>8
D、x≥6且x≠8
19.如图所示，该几何体的俯视图为（ ）。
A、
B、
C、
D、
20.当2<a<3时，代数式|a-3|+|2-a|的值是（ ）。
A、3
B、1
C、-1
D、-3
21.满足不等式组
的x取值范围为（
）。
A、x<5
B、x≥3
C、x≥5
D、3≤x<5
22.超市店庆促销，某种书包原价每个x元，第一次降价打八折，第二次降价每个又减10元，经两次降价后价格为100元，则得到方程为（ ）。
A、0.8x-10=100
B、0.08x-10=100
C、100-0.8x=10
D、x-0.8x-10=100
23.已知实数x，y满足
则以x，y的值为两边长的等腰三角形的周长是（
）。
A、12
B、15
C、12或15
D、以上均不正确
24.互联网“微商”经营已成为大众创业新途径，某微信平台上一件商品标价为200元，按标价的五折销售，仍可获利10元，则这件商品的进价为（ ）。
A、110元
B、100元
C、90元
D、80元
25.实数a，b在数轴上对应点的位置如图所示，化简
的结果（
）。
A、-3a+b
B、3a-b
C、a-b
D、b-a
26.不等式
的大于1整数解的个数是（
）。
A、1个
B、2个
C、3个
D、4个
27.已知x-2y=3，那么代数6-2x+4y的值是（ ）。
A、0
B、3
C、6
D、9
28.某班学生去距离学校10千米的博物馆参观，一部分学生骑自行车先走，过了20分钟后，其余学生乘汽车出发，结果他们同时到达，已知汽车的速度是骑车学生的2倍，设骑车学生的速度为x千米/小时，则所列方程正确的是（ ）。
A、
B、
C、
D、
29.下列算式：①
；②
；③
；④
；⑤
；运算结果正确的概率是（ ）。
A、
B、
C、
D、
30.在△ABC中，∠ACB=90°，AC=12，AB=13，DE垂直平分AC交AC于点D，交AB于点E，则DE的长为（ ）。
A、5
B、4
C、3
D、
31.若x=-2是关于x的一元二次方程
的一个根，则a的值为（ ）。
A、-1或4
B、-1或-4
C、1或-4
D、1或4
32.已知点M（1-2m，m-1）在第四象限，则m的取值范围在数轴上表示正确的是（ ）。
A、
B、
C、
D、
33.设A（a，b）是正比例函数
图像上的任意一点，则下列等式一定成立的是（
）。
A、3a-4b=0
B、3a+4b=0
C、4a-3b=0
D、4a+3b=0
34.若关于x的一元二次方程
有两个不相等的实数根，则k的取值范围是（
）。
A、k<6
B、k<6且k≠2
C、k≤6且k≠2
D、k>6
35.直线y=kx+3经过点A（2，1），则满足不等式kx+9≥0的取值范围为（ ）。
A、x≤9
B、x≥9
C、x≥-9
D、x≤3
36.某校九年级（1）班全体学生2018年初中毕业体育考试的成绩统计如下表：
根据上表中的信息判断，下列结论中错误的是（ ）。
A、该班一共有40名同学
B、该班学生这次考试成绩的众数是45分
C、该班学生这次考试成绩的平均数是45分
D、该班学生这次考试成绩的中位数是45分
37.已知3是关于x的方程
的一个实数根，并且这个方程的两个实数根恰好是
RtΔABC的两条直角边的边长，则∆ABC的内切圆的面积为（ ）。
A、9 π
B、4 π
C、2 π
D、π
38.一枚质地均匀的骰子，其中六个面上分别标有数字1，2，3，4，5，6，投掷一次，朝上一面的数字是奇数的概率为（ ）。
A、
B、
C、
D、
39.为迎接“义务教育均衡发展”检查，某市抽查了某校七年级8个班的学生人数，抽查数据统计如下：52，49，56，52，51，55，54，这组数据的极差是（ ）。
A、7
B、-7
C、±7
D、5
40.已知等边三角形的边长为3，点P为等边三角形内任意一点，则点P到三边的距离之和为（ ）。
A、
B、
C、
D、不能确定
41.关于x的一元二次方程
有两个相等的实数根，则锐角α等于（
）。
A、15°
B、30°
C、45°
D、60°
42.如图，将∆PQR向右平移2个单位长度，再向下平移3个单位长度，则点P平移后的坐标是（
）。
A、（-2，-4）
B、（-2，4）
C、（2，3）
D、（-1，-3）
43.下列语句正确的是（ ）。
A、对角线互相垂直平分的四边形是菱形
B、对角线相等的四边形是矩形
C、有两边及一角对应相等的两个三角形全等
D、平行四边形是轴对称图形
44.如图，在平行四边形ABCD中，BF平分∠ABC，交AD于点F，CE平分∠BCD，交AD于点E，AB=6，EF=2，则BC长为（ ）。
A、8
B、10
C、12
D、14
45.如图，过反比例函数
（x>0）的图像上一点A作AB垂直x轴于点B，连接AO，若
，则k的值为（
）。
A、-2
B、1
C、2
D、±2
46.如图，AB//CD，BP和CP分别平分∠ABC和∠DCB，AD过点P，且AD与AB垂直，若AD=8，点P到BC的距离是（ ）。
A、8
B、6
C、4
D、2
47.二次函数
（a≠0）的部分图像如图所示，图像过点（-1，0），对称轴为直线x=2，下列结论：①4a+b=0；②9a+c＞3b；③8a+7b+2c＞0；④若点A（-3，
）、点B（
，
）、点C（
，
）在该函数图像上，则
；⑤若方程a（x+1）（x-5）=-3的两根为
和
，且
，则
，其中正确的结论有（ ）。
A、2个
B、3个
C、4个
D、5个
48.如图，在矩形ABCD中（AD＞AB），点E是BC上一点，且DE=DA，AF⊥DE，垂足为点F，在下列结论中不一定正确的是（ ）。
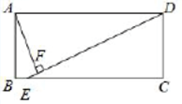
A、
B、
C、AB=AF
D、BE=AD-DF
49.如图，点D（0，3），O（0，0），C（4，0）在⊙A上，BD是⊙A的一条弦，则sin∠OBD为（ ）。
A、
B、
C、
D、
50.如图，△ABC与△A’B’C’都是等腰三角形，且AB=AC=5，A’B’=A’C’=3，若∠B+∠B’=90°，则△ABC与△A’B’C’的面积比为（ ）。
A、25：9
B、5：3
C、
D、
二、解答题。根据题目要求，回答问题。（共2小题，第51题10分，第52题12分，共22分）
51.如图，点D是AB上一点，DF交AC于点E，DE=EF，FC//AB。
求证：AE=CE。
（一）
某公司计划从甲、乙两种产品中选择一种生产并销售，每件产销x件，已知产销两种产品的有关信息如下表：
其中a为常数且
。
52.若产销甲、乙两种产品的年利润分别为万元，万元，直接写出，与x的函数关系式；
三、案例分析题。阅读材料，回答问题。（共1小题，每小题1分，共14分）
53.分别求出产销两种产品的最大年利率；
54.为获得最大年利率，该公司应选择产销哪种产品？请说明理由。
55.以下是《直线、射线、线段》中的一课的教学片段：
师：同学们，你们在小学阶段己经学过了直线、射线与线段，现在回忆一下，再相互讨论一下他们的区别与联系。
（学生们议论纷纷，3分钟后，老师让同学们安静下来。）
（接着，老师从头上拔下一根头发，同学们很惊奇地看着老师。）
师：大家刚才讨论了直线、射线与线段的区别与联系，这个头发是直线、射线、线段中的哪一种？现在小组讨论后组员代表分别说说。
（2分钟后，各组员代表举起了手。）
生1：我们小组经过讨论认为该头发是一条射线，其中毛囊是射线的端点，发梢可以无限延伸。
生2：我们小组认为该头发是一条线段．既然头发己经拔下来了，那它也不长了。
师：挺好的，从头发拔下来不再长了这一角度看，是一条线段，从头发还可以再长这个角度看，又是一条射线，还有其他意见吗？
生3：我们小组经过讨论认为老师的问题有错误，该头发既不是线段、射线也不是直线，而是曲线，因为老师没有把该头发绷紧。
（学生们大笑起来，老师也微笑着环顾同学们。）
师：真是后生可畏，老师们真为你们有这种质疑的精神而点赞，你们小组认真严谨的学习态度征服了我，俗话说：长江后浪推前浪。和大家一起探索数学的奥秘，老师也收获不少，真是谢谢大家！
根据以上材料，回答下列问题：
1.对生3小组敢于质疑和批评教师这种行为阐述你的看法；
2.简述如何做好小学与初中衔接内容的教学；
3.在数学课堂教学中，如何更好地实施分组讨论教学。
四、教学设计题。请根据所提供的教学材料和相关情况，按要求完成教学设计。（共1小题，每小题1分，共14分）
56.撰写说明：以下两例为教学内容，撰写“锐角三角函数——正弦“教学设计片段。
（学生已学知识：直角三角形中，30°角所对的边等于斜边的一半，等腰三角形的性质，相似三角形的性质。）
撰写要求：
写出本教学设计片段，并说明其设计意图；
不要求写出例题的解答过程。
【例1】如图1，在Rt△ABC中，∠C=90°，∠A=30°，BC=35，求AB。
【例2】如图2，容易画一个Rt△ABC，使∠C=90°，∠A=45°，计算∠A的对边与斜边的比
，由此你得出什么结论？
注：篇幅有限，答案及解析请下载试卷后查看。