教师资格初中数学真题及答案解析（2022上半年）
一、单项选择题。单项选择题（本大题共8小题，每小题5分，共40分）
1.极限
的值是（ ）。
A、0
B、1
C、2
D、无限
2.已知向量a和b，
，
，
，则
的值是（ ）。
A、-7
B、-1
C、1
D、7
3.行列式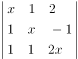
表示的系数中，一次的系数是（ ）。
A、-3
B、-2
C、2
D、3
4.同时投掷一枚硬币和骰子，硬币正面朝上且骰子点数大于4的概率是（ ）。
A、1/6
B、1/3
C、1/2
D、2/3
5.对于定义在R上的函数，下列结论一定正确的是（ ）。
A、奇函数与偶函数的和为偶函数
B、奇函数与偶函数的和为奇函数
C、奇函数与偶函数的积为偶函数
D、奇函数与偶函数的复合函数为偶函数
6.已知矩阵
则求得PQ是（ ）。
A、
B、
C、
D、
7.下列数学概念中，用“属概念加和差”方式定义的是（ ）。
A、正方形
B、平行四边形
C、有理数
D、集合
8.下列数学成就是中国著名数学成就的是（ ）。
①勾股定理
②对数
③割圆术
④更相减提术
A、①②③
B、①②④
C、①③④
D、②③④
二、简答题。简答题（本大题共5小题，每小题7分，共35分）
9.某支舞蹈队有4男6女，从中选3人参加比赛，如选到1名男，2名女的概率？
10.已知函数
，求
在
的二阶导数
。
11.已知
，设
为
阶矩阵，
为阶单位矩阵，若可逆，试用表示；若不可逆，说明理由。
12.简述研究二次函数
单调性的两种方法。
13.画出数轴并指出解释
有无穷多个。
三、解答题。解答题（本大题1小题，10分）
14.对平面上的任意三点
，
。
给出如下定义：
（1）若
，
，
，求
与
的值。（4分）
（2）判断与三角形ABC的面积S的关系，只写出来结果。（3分）
（3）在（1）的条件下，若点
是以
为圆心的单位圆上的动点，求
的最大值。（3分）
四、论述题。论述题（本大题1小题，15分）
15.论述数学史在教育教学各阶段（导入、探索、应用）的作用。
五、案例分析题。案例分析题（本大题1小题，20分）阅读案例，并回答问题。
（一）
在一元二次方程概念教学导入环节中，甲乙两位教师设计了如下问题：
（甲）问题1：同学们知道哪些方程(组) ？
问题2：你能类比一元一次方程的定义给出一元二次方程的定义吗？
问题3：请每位同学各自写出两个一元次方程，若用一个式子表示所有一元二次方程，你会用什么来表示呢？
（乙）问题1：根据下列问题思考：
①圆的面积为16，求其半径
；
②要组织一场篮球赛，参赛任意两个队之间都要比赛一场，赛程计划7天，每天4场， 要邀请个队参加，求；
③用一条长40cm的绳子围成一个面积为75平方厘米的矩形，求矩形的长。
问题2：观察列出的3个方程，它们有什么共同特征？
16.（1）写出教师乙提出问题中的三个方程； (6分)
（2）分别指出各自的优点，并谈谈问题情境在教学中的作用。(14分)
六、教学设计。教学设计题（本大题1小题，30分）
（二）
平行线的判定
根据平行线的定义，如果平面内的两条直线不相交，就可以判断这两条直线平行但是，由于直线无限延伸，检验它们是否相交有困难，所以难以直接根据定义来判断两条直线是否平行，那么，有没有其他判定方法呢？
思考：我们以前已学过用直尺和三角尺画平行线(图5.2-5) ，在这一过程中，三角尺起着什么样的作用？
简化图5.2-5得到图5.2-6，可以看出，画直线AB的平行线CD，实际上就是过点P画与
相等的
，而和正是直线AB、CD被直线EF截得的同位角，这说明，如果同位角相等，那么AB//CD。
一般地，有如下利用同位角判定两条直线平行的方法：
判定方法1两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行。简单说成：同位角相等，两直线平行。
17.（1）说出其它判定方法，并使用判定方法1证明；（8分）
（2）写教学设计，包含教学目标、重难点、教学过程。（指导教学的活动及设计意图）（22分）
注：篇幅有限，答案及解析请下载试卷后查看。